啥叫随机(风花雪月钓鱼经验增加为什么随机性会让玩家不爽?揭开随机性背后的“难言之隐”)
文/猴与花果山
我们玩过很多游戏中都有随机数,但是一些游戏的随机数总是让人有不爽的感觉,很奇怪的是明明有问题,但又很难说清问题在哪儿。所以今天我们就从游戏设计的方法出发,来看看一个游戏在设计过程中的一些细节与随机性之间的矛盾,从而挖掘出这些让人不爽的随机性背后的“难言之隐”。
01 游戏设计是在设计多叉树
其实我们可以把游戏的过程设计,或者玩家体验游戏的过程,看作是一颗多叉树:

在这颗多叉树上有这样几种节点:
根节点:即玩家第一次与游戏交互(产生操作)的节点。在根节点之前,由于玩家和游戏没有交互,所以游戏中一切的“发展”都是一种“演示”,无法形成“玩”的概念,只有当玩家做出了操作以后,并且操作“推动”了游戏的进程,这才能算是真的开始玩游戏了。这也是为什么很多游戏要有一个“Push Start Button”界面的原因。

大多游戏都有一个“欢迎画面”需要玩家点一下才继续
节点:即影响游戏局面的事件的发生点,一个节点会引申出多个子节点,每局游戏运行过程中会根据这个节点的发生的具体事件的具体内容来决定这局游戏具体通向其中哪一个子节点。通常来说,可以影响游戏局面的因素包括且不限于玩家的操作、关卡中预设的元素、突发事件、随机事件等元素。即在游戏运行过程中动态产生了一些情况,这些情况导致游戏局面发生变化,比如下象棋时每次落子都是一个节点,它会导致棋局进入不同的节点(产生不同的局面)。我们可以把节点理解为一个函数y=f(x),因变量y是要通向的下一个节点,而参数x是一个集合,是当前状况下所有影响局面变化的元素产生的一个集合。比如“模拟高尔夫球”游戏,我们打一杆球就是一个函数(节点),参数x有我们击球的角度、力度、用的杆,这些来自玩家操作;还有球场的风力、风向等来自游戏运行时的环境,然后根据这些参数,运行了y=f(x),得出了y,即“球落在了哪儿,游戏是否结束(进入结束节点)?如果没有结束就要打下一杆(进入新的节点)。

围棋每落一个子都是一个节点
结束节点:当进入这个节点的时候,一局游戏就结束了。对于某一个玩家而言,这个节点存在好坏关系,即这个节点代表了该玩家“获胜”,就会是个“好结局”。
玩家玩一局游戏,就是在一棵多叉树上走了一枝:

这一次玩家走了这一枝,下一次也许就未必了。根据上面的介绍我们不难理解——在一局游戏中玩家在这颗多叉树上具体能走过哪些节点,取决于每一个节点函数的运行结果。而玩家努力找寻或者操作是为了能走上一条通向“好结局”的路线,一个游戏可以有多个“好结局”的结束节点,通向同一个“好结局”的路径也最好能是多条的。“好结局”或者“通向好结局的路径”越少(占多叉树的比例),玩家越会觉得游戏困难;“通向好结局的路径”越是单一,游戏越是显得有“最优解”。
多叉树是一种设计的思想,你没法在每次设计时候都画出多叉树,因为那穷举量太大了,但是你必须在脑海中构建出多叉树来,至少每一个节点的下一个节点会是哪些你应该能清晰的抽象出来。
02 用多叉树看一些游戏
九宫棋(Tic Tac Toe)

九宫棋是A和B两名玩家进行的游戏,规则也非常简单——轮流行动,直到一方连起一条直线上3个棋子。因此九宫棋的两种节点分别是:A玩家行动节点和B玩家行动节点,在这些节点里的参数只有:当前玩家决定落子在哪儿,最后函数返回出新的棋局——通向了新的节点或是达到了结束节点。
我们先把九宫棋的格子做一个编号,然后我们来看九宫棋的玩家在这个游戏里经历的多叉树(为了更好地说明问题,我们附加一个条件,即先行的A玩家第一个棋子必须落在B2,当然事实也是B2也是绝大多数A玩家会选择的第一步落点):

从这个图中我们可以看出:
每个玩家落子都是一个节点(红色代表A玩家,蓝色代表B玩家)。
红色粗线的路线代表A玩家“通向好结局的路径”。
一局游戏经过的节点深度,取决于双方玩家一起连出的路径。
保龄球(Bowling)

一种室内运动,把一个球滚过一段木板轨道,将另一端的瓶子击倒。
我们说九宫棋是一个回合制游戏,可以清晰地看到他的多叉树,保龄球是一种运动类游戏,但也有多叉树,只是相比九宫棋“深度”(即层数)更低,但“广度”(同一个节点延伸出的节点数)高非常非常多。

从上图红色箭头我们可以看出,因为保龄球可以丢的角度接近于无限多个,而保龄球(图中绿色的球)的起始位置也是在图中蓝色线段上的任意一点,所以在“投球”这个节点上,而因为是“电子游戏”,所以我们可以忽略掉抛球的力量手法等因素(确保每次都能是一样的固定值),光是位置和角度就可以延伸出接近无穷多个子节点,每一个节点都通向一个结束节点,其中很多个结束节点是“好节点”(所有的瓶子倒了,不管倒成什么形状,只要倒下)

保龄球的多叉树就是如此——丢出保龄球的节点,引申出无限多子节点,但是每个节点都会带来一个结束节点,因为在这中间没有其他因素去改变整个局面了,球最终能打中几个瓶子、瓶子最终有几个会倒下,仰仗于物理学和计算机的算力,我们其实可以在球丢出的那一瞬间,就用计算机算出精确的结果了。
那如果我现在要为我的《手机版保龄球游戏》追加一些有趣的元素,让这些元素改变保龄球的固有玩法可以怎么加?最简单的一个就是——为一些情况追加一层深度:现在我们把木板两边的坑道换成“随机反射装置”(因为电子游戏是虚拟的,所以可以出现现实中无法出现的,不可思议的有趣元素),这个装置不会干扰球的运动速度,但是会让重新随机一个角度作为球滚动的新方向,从而导致球的轨迹(核心元素)发生变化:

如上图所示,红色的是保龄球丢出时候的方向,当碰到墙壁后,保龄球的轨迹可能变成2根蓝色箭头夹角中的任意一个角度(取决于当时的随机数)。这样一来我们的《手机版保龄球游戏》与现实的保龄球就不再一样了,它多了一个新的玩法:

迷宫\随机迷宫游戏
很多游戏中都有迷宫,既然是迷宫就会有分叉路,一些路通向终点,而一些路通向死胡同。
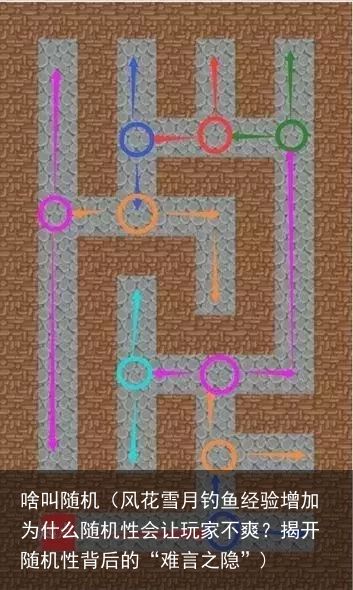
迷宫只是多叉树的一种表现方式而已,骨子里就是一个多叉树。迷宫中每个分叉口都是一个节点,由这个节点引申出后续的分叉口(节点),根据这些分叉路线,我们再来进行布怪和放置奖励、终点的工作。
03 节点的设计
在这个多叉树的设计里,最重要的一环就是节点的设计,因为每一个节点就是游戏规则中至关重要的一步(或者可以理解为“一个转折”)。
就像我们之前说的——可以把一个节点看作是一个函数,顺着这个解说下去就是:一个节点有3个核心元素组成:
参数(自变量):即这个节点中影响游戏局面的“动态”元素,这通常是来自玩家操作或游戏运行时算出来的一些数据。设计师在设计每个节点的时候,同时影响这个节点的因素都可以是这个“函数”的“参数”,如猜拳时,需要双方同时输入出的拳,就是2个参数。参数中,玩家的操作通常可以理解为“从很多选项中选出来的那个”,而不是“可供选择的选项”。返回值(因变量):即当前游戏的局面,以及由此产生的下一个节点。函数本体(运行逻辑):当传入参数后,进行运算获得返回值的过程,或者更直白的说就是“游戏规则”,比如猜拳的时候,函数本体就是判断双方的出拳,决定谁赢谁输或者平局(即下一个节点是谁)。当一个节点的参数中有“玩家控制”的因素的时候,即这是根据玩家行为得出的一个结果的时候,我们可以把它理解为一个“可控节点”,否则就是个“变化节点”或者叫做“不可控节点”。很好理解的是——“可控节点越多”,玩家对游戏进行的把控度也就越高。当一个“可控节点”下所有的子节点都没有“可控节点”,且都会链接到一个非“好结局”的“结束节点”上时,我们称这个可控节点为“死节点”。
玩家玩n次(n趋向于无穷大)这个游戏,在同一个可控节点上,每次玩都“输入”同样的参数(并且其他因素输入的此参数也不变)时,如果最终总能通向一个固定的结束节点,而这个结束节点的所有参数都是完全一致的,我们称这个游戏是“可解”的,否则这个游戏“不可解”。上面说过的九宫棋是“可解”的,因为只要双方每次都按一个顺序走,那么每次结果都是一样的(结果不仅仅是谁获胜,还有棋盘上所有棋子的位置,因为具体谁获胜,是依赖于棋盘上所有棋子位置来算出的,而并非一个简单属性);同样,原始的保龄球也是“可解”的,只要能保证每次丢球的起点、角度等都完全相同(只是人类基本做不到)结果也必然是一样的;但是当保龄球加入我们刚才说的“随机反射装置”后,就变成“不可解”了,因为每次随机数的结果是不同的,因此我用一样的方法(位置、角度)丢出n次,会得到n个不同的结果,其中只有个别的可能会相等。所以这里有一个关键在于对结束节点,或者说是对游戏的“结果”的数据结构的抽象——很多时候“输了”“赢了”都只是一个“基于规则的推理”,而根本不属于“结果”,比如五子棋,棋盘上所有棋的位置才是结果,因为所有棋的位置中出现了5个连在一起的,又因为规则规定5个子连在一起就是胜利,由此我们“推理”出了一方获胜。
04 玩家在游戏中进入“可控节点”
通常来说,玩家进入某个“可控节点”的方式只有2个:
决策进入:即在一个“非可控节点”的结果中存在一个选择,玩家的选择直接走向一个可控节点,大多策略类、养成类、益智类和GalGame玩法的游戏就是如此。比如一个三国游戏,战斗结束后我们处理俘虏:

大多三国类游戏,在战斗结束后都会有这么个“小型游戏”,它的多叉树是这样的:
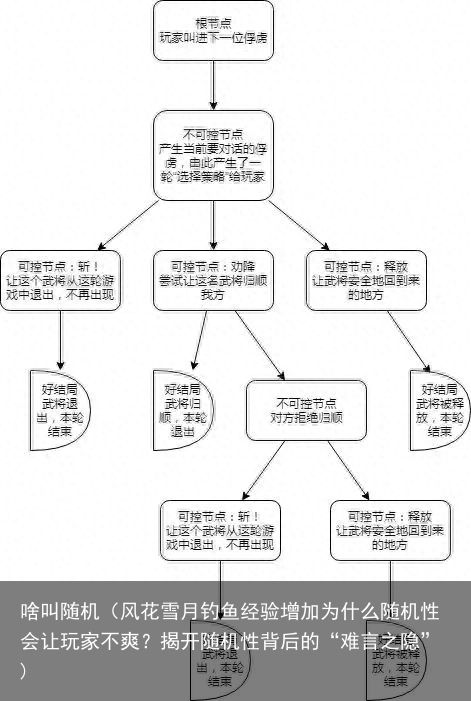
中间的3个可控节点(斩、劝降、释放),来自同一个不可控节点产生的一个选择。
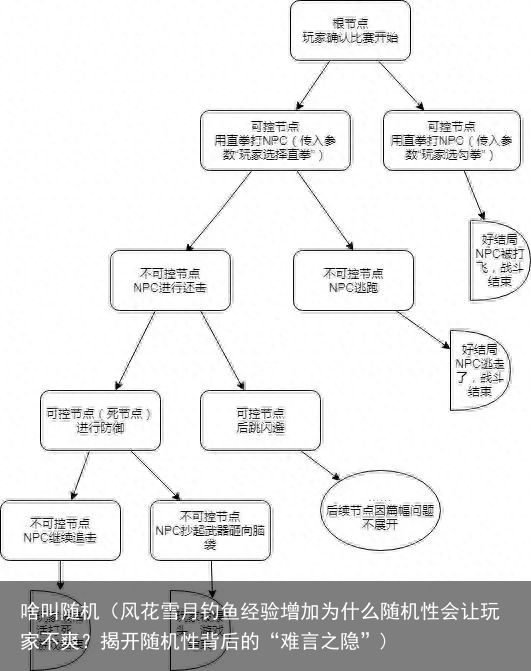
技巧进入:玩家进入一个节点是因为使用了一些操作类的技巧,游戏中的QTE小游戏都是典型技巧进入的方式,玩家知道哪个节点通向“好结局”,甚至知道“最优解”,但是必须要通过技巧测试,才可能达成,如果反应和水平不够,就可能会掉入“死节点”。

在火纹风花雪月中,钓鱼就是一个QTE小游戏
05 放哪儿都尴尬的随机性
如果我们用随机来决定节点通向的下一个节点,这不仅会把“可控节点”变成了“不可控节点”,还会让游戏失去“可解”特性。
我们看过很多文章和书籍,都告诉我们“游戏之所以吸引人,因为有2个要素——其一是准确的反馈,其二是学习成长”。所谓准确的反馈就是当我们做了一个事情的时候总能得到一个相对的反馈,而其中的一些反馈是好的,一些反馈是糟糕的,从设计的角度出发看,这就是在游戏这颗多叉树上,玩家寻找的是“好结局”对应的结束节点;所谓学习成长,即玩家从游戏中掌握了一些技巧和经验,由此可以使得自己技术更精妙,更容易获得“好结局”。
事实上玩游戏的过程,就是在解一道题,因为这道题非常的复杂(我们可以看到上面所有的多叉树都没法列全,打草稿都如此困难,更何况人脑直接计算),所以我们没法看清所有的解,所以我们需要一步一步的探寻下去,在这个过程中不断享受发现带来的乐趣;当然一些技巧类游戏,如动作游戏,可能我们最先就知道了最好的路径,只是我们的操作技巧没法一次性把我们送到最好路径上,或者有些技巧我们掌握不了(过于困难)以至于只能另寻他路。而玩游戏的经验,正是帮我们克服“算力不足”(导致一次看不到所有的解)的最好“老师”,而游戏“可解”是这一切的基石,因为“不可解”的游戏没法积累经验,比如微信抢红包,没有任何经验可以帮助你下一个红包抢到你所期望的某个数额,因为微信抢红包的过程中有随机数决定下一个节点的情况存在:
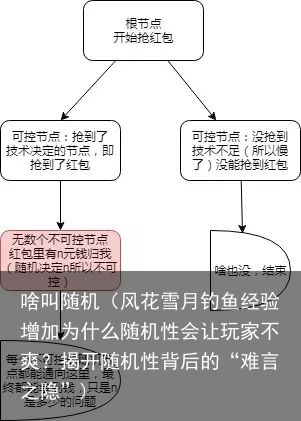
不难理解,上图红色的部分是因为“随机性”产生的无数个“不可控节点”,而每一个这种节点都能带出一个结束节点,结果都不一样(只是偶尔可能会有值相等的情况),所以抢红包“不可解”,并且由此你没法训练一种技巧或者思路来做到“每次都能抢到n=100的红包”。
事实上所有棋类游戏的“棋谱”都是经验的记录,只是很多棋类游戏即使是棋谱也过于庞大,人脑依然无法记录,以至于还是需要人动脑筋去探索,才保持着乐趣——事实上Alpha Go可以战胜世界围棋高手,正是因为围棋“可解”,只是人脑的算力不足,而Alpha Go的算力完美符合需求;相反的例子是九宫棋,因为就连小孩子也能很快学会记住必胜或必定不胜的方法(即过程路径),所以游戏性就大跌。所以好的游戏,应该是一个极其庞大的多叉树,其中有非常多的“混淆”导致玩家看不清所有的解,也很难在第一时间确定最佳解,即使相对容易知道最佳解的,也可以在技术上(包括时间限制、操作水平要求等方面)做功夫,让玩家并不是轻而易举的就能看破。但是,这种“不能看破”与“完全无理由预测”是完全不同的东西,虽然从某个角度看结果都是“玩家难以控制”。
所以游戏的随机性,如果运用在导致整个游戏多叉树“不可解”的情况下,那这个用法就是不好的,典型的就是将随机作为决定结果的因子,比如现有游戏中的“抽卡”系统,都是不好的设计,玩家并没法从这个系统获得任何乐趣(即学不到技巧,也没法积累经验),当然抽卡还是会让玩家高兴,因为抽到了好东西,但这让玩家高兴的是奖励,而不是游戏本身。
06 不好的随机性会让玩家面临“所有可控节点都是死节点”的尴尬
还有一种极为“精妙”的随机数用法,是用于约束“可控节点”的范围,通常会出现在一些卡牌玩法的游戏中。举个例子:我们把猜拳游戏改进一下,变成单人游戏——现在发3张小卡片给玩家,每张小卡片上写有“石头”“剪刀”或“布”的一个,玩家出小卡片来代替出拳,而“对手”会出的也是从小卡片中抽一张出来直接放在桌上,玩家要做的就是从3张小卡片中选出一张来和这张抽出来的小卡片进行“猜拳”。这时,由于3张小卡片是随机发给玩家的,即玩家有可能拿到3张“石头”,因此在这个猜拳游戏中,玩家只能出“石头”,而不能出“布”或“剪刀”,而桌面上那张“对手”如果是“布”,那么玩家此时面临的局面就是一个“所有可控节点都是死节点的情况”:
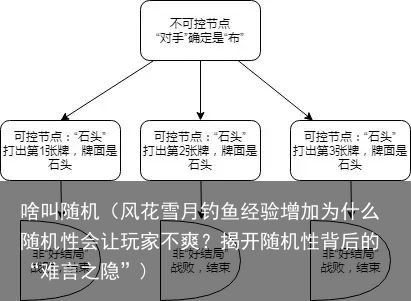
无论怎么选都到不了“好结局”,这还能有趣吗?当然扯开说一句,这也正是很多FPS游戏提供一把小刀给玩家的核心原因——当玩家子弹打完之后只能选择坐以待毙是很烂的游戏体验。
由此我们可见,如果要在控制“可控节点”的选择范围上下文章,我们的“随机机制”至少要保障并不是所有的“可控节点”都是“死节点”,这个算法会相当复杂,但并不一定做不出来。
07 随机性与游戏性关系的归因谬误
可见随机数很难用于游戏设计中,我们大多游戏设计的随机都是不好的,只是玩家“感觉不到”或者即使感觉到了,也说不清楚为什么不好而已。“随机性会为游戏带来乐趣”这个观点本身是一个“基本归因谬误”误,上面我们也证明了——“随机性”跟“游戏有乐趣的元素”几乎格格不入,唯一能很困难地插入随机数的地方也没法证明随机数能带来好玩。我们把获得奖励的喜悦错误地当做了是“抽奖机制”给出的喜悦,事实上随机数给人带来的喜悦和心理期望有非常大的关系——有AB两个员工,A员工期望工资是10K,B员工期望工资是12K,公司的机制是基本工资10K,奖金0-2K随机,所有同事一视同仁——月底A和B都拿到了11K的收入,A是高兴的,因为超越了他的期望,B是不爽的,因为没有达到期望——正因为人有期望,所以随机会带来所谓的情绪波动,而你给Alpha Go玩这个发工资小游戏,再怎么地它的心理都不会波动一下。
总结
当我们看清了设计原理之后,就不难发现——随机性并不能给游戏带来什么乐趣,甚至会使得游戏乐趣降低,更不可能“带来思考深度”,因为一旦随机了,就没有任何“思考”可言(经验和技巧都派不上用)了。游戏中让人别扭的随机数,正是因为玩家体验到了“我做出了最大的努力接近最佳路线,但当我走到结束节点的时候发现,这个节点是不是一个好结局是随机决定的”,即——随机性让付出和反馈变得不一致。